Using adjusted means to correct for different sample replication in sensory tests.
Have you ever wondered why sometimes the mean scores are presented in results tables under the heading ‘Adjusted Means’…?
Well if so, there is a good reason that means are adjusted!
Think of the following scenario:
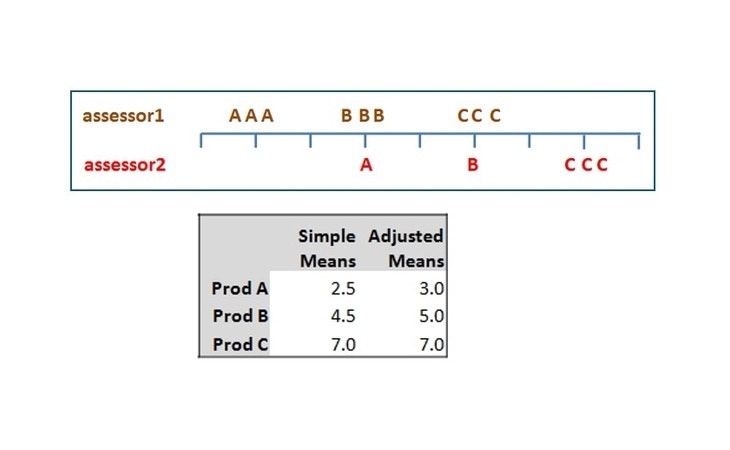
Assessor 2 has a car that often breaks down, meaning she can’t make the testing session. But she is a good assessor, so we still want her data. In the picture below, owing to these missed sessions, Assessor 2 has only provided a single score for products A & B although all 3 sessions worth of data for product C.
Assessor 1 however, is much more reliable and has provided all data.
So what can we do? If we look at the scale, it can be seen that Assessor 2 generally scores 2 units higher than Assessor 1, so if we calculate the mean scores for each product with the data as it is, we will find that the simple mean scores for products A & B are half a unit lower than they would be, had all 3 replicates been available. (Try it out!)
In this situation it is better to correct for the imbalance in the data by using adjusted means. If the simple means are relied on, then the interpretation of results may be wrong since product differences A vs C and B vs C would be half a unit larger than they should be!